A case study: RSA

What will this section cover?

• What is Simple Power Analysis?
• What is the RSA algorithm?
• How can you break implementations of RSA using Simple Power Analysis?

RSA is an encryption algorithm that is used all over the place. That little padlock in your browser; it is powered by RSA. Coding an implementation of RSA is reasonably simple, but the mathematics behind it can prove to be really though. Luckily, there is no need to dive too much into the mathematics to crack RSA using Simple Power analysis. In the chapter on AES, we will go a bit deeper into cache-based Power analysis attacks, why they work exactly and how to perform them on the ChipWhisperer. This chapter is going to skip over a few of the specifics to create a better overview of our method and goals.

What is Simple Power Analysis

Simple Power Analysis (also known as SPA) is a way of leaking information from power measurements of a microprocessor. One can imagine that a microprocessor in idle will use less power than a microprocessor running instructions at maximum speed. Similarly, some processor instructions use more power than others or use power at different intervals. If we take a series of power measurements of a microprocessor performing an algorithm, we use therefore possible say something about the instructions that processors performed. The technique of looking at such power measurements and leaking information from them is called Simple Power Analysis.

We are going to exploit this technique with an encryption algorithm called RSA. In some software implementations of RSA, we can leak secret information just by looking at power measurements of the microprocessor.

What is RSA?

RSA is an algorithm used to do asymmetric encryption. This means we have two distinct keys. Most of the time this means we have one key to encrypt plain text to cipher text, one key to decrypt cipher text back to plain text. It is common to have one of these keys be publicly available while the other is kept extremely private. Because of this, it is also called the public and private key cryptography.

RSA uses one simple principle. For encryption with public key \( e \), for every byte of our plain text \(b_i\) we have encrypted byte \( c_i=b_i^e \) modulo some integer \( N \). For decryption with private key \( d \), for every byte of our cipher text \(c_i\) we have encrypted byte \( b_i=c_i^d \) modulo some integer \( N \). The specific relationship between these numbers is not as important for now.

When one learns that usually the minimum key length for the private key is 1024 bits, one might wonder how these computations are actually done on the bare hardware. It turns out that we can interpret modulo exponentiation as repeated multiplication and squaring alternated with modulo division. This is how that works.

If we are given an enormous number \( x \), and we are tasked with the raising it to the 13th power, we might do it as follows:

\[ x^{13} = x^8 \cdot x^4 \cdot x^1 \]

This is part of the method of Modular Exponentiation. Notice that \((13)_{10} = (1101)_2\). There are some ties with powers of 2 here. Thus, we might write a custom power function in Python as the following.

# Custom implementation of pow(x, y)
def custom_pow(x, y):
    res = 1

    # Until we have reached the highest power
    while (y > 0):
        # If the last byte is a one
        if (y & 0x01):
            res *= x

        # Move on to the next byte
        y >>= 1
        x *= x

    return res

If we add a modulo into our function, we have essentially created a function to do RSA encryption. This is also often how the pseudocode for lower level implementation looks like.

# Custom implementation of pow(x, y) % p
# With p >= 2
def custom_pow_mod(x, y, p):
    res = 1

    # Until we have reached the highest power
    while (y > 0):
        # If the last byte is a one
        if (y & 0x01):
            res *= x
            res %= p # Make sure we stay modulo p

        # Move on to the next byte
        y >>= 1
        x *= x
        x %= p # Make sure we stay modulo p

    return res

Note: This is in fact also how most arbitrary precision library implement raising to the power. This is due to the (relatively) low maximum complexity of this calculation.

If you are already a small bit familiar with Side-Channel Analysis and Power Analysis, you might immediately see what is going wrong here. If you don't see it immediately, let us go through it together.

When we do Power Analysis, we get the power consumption of a microprocessor for a given amount of time. Let us say we would have a computer which purely executing the computation for custom_pow_mod(3, 5, 15). The steps that are taken in this computation are done noted below. Take a look at that the computation and verify it in your head.

custom_pow_mod(3, 5, 15):

res := 1

# Round 1

# [A]
y > 0 = 5 > 0 is true, thus:
    y & 0x01 = 5 & 0x01 is 1, which equals true, thus:
        # [B]
        res := res * x = 1 * 5 = 5
        res := res % 15 = 5 % 15 = 5

    # [C]
    y := y >> 1 = 5 >> 1 = 2
    x := x * x = 3 * 3 = 9
    x := x % 15 = 9 % 15 = 9


# Round 2

# [D]
y > 0 = 2 > 0 is true, thus:
    y & 0x01 = 2 & 0x01 is 0, which equals false

    # [E]
    y := y >> 1 = 2 >> 1 = 1
    x := x * x = 9 * 9 = 81
    x := x % 15 = 81 % 15 = 6

# Round 3

# [F]
y > 0 = 1 > 0 is true, thus:
    y & 0x01 = 1 & 0x01 is 1, which equals true, thus:
        # [G]
        res := res * x = 5 * 6 = 30
        res := res % 15 = 30 % 15 = 0

    # [H]
    y := y >> 1 = 1 >> 1 = 0
    x := x * x = 6 * 6 = 36
    x := x % 15 = 36 % 15 = 6

# Round 4

# [I]
y > 0 = 0 > 0 is false.

# [J]
Result: 0

One might notice that not every round contains the same amount of steps, and thus, we might imagine that the power consumption of our machine looks similar to Figure 1.

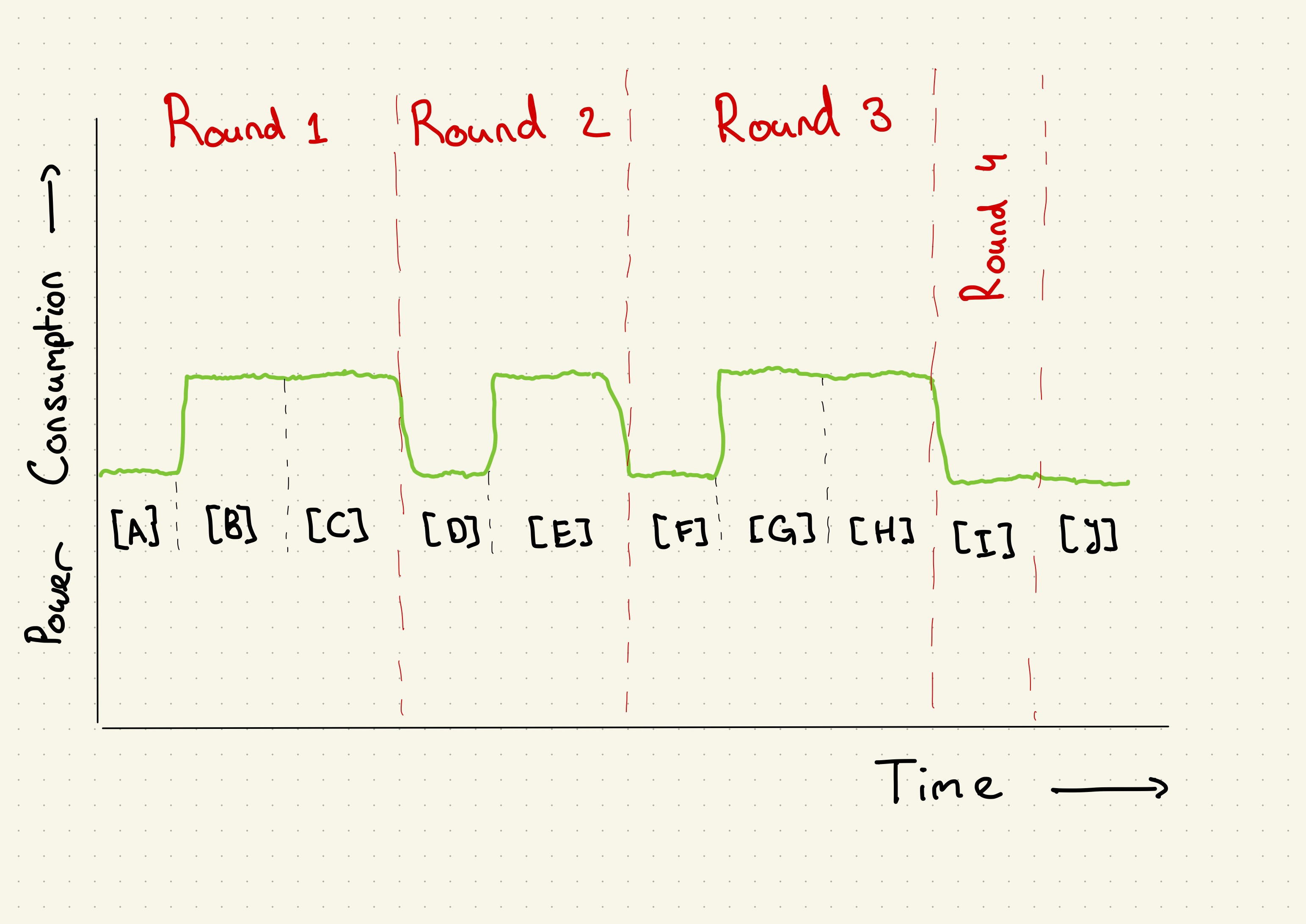
Figure 1: A projected power trace for the custom_pow_mod(3, 5, 15) function call.

Note: This sketch uses the estimate that conditionals and loops (if and while) are less power consuming than normal numerical calculations (>>, * and %), which isn't trivially true, but for the sake of simplicity we are going to assume it is true.

You might notice that given this sketch, we can reconstruct some information about the argument y provided to the custom_pow_mod function. We start with a long spike, thus, the binary number representation of y starts with a 1. This is followed by a short spike, which indicates a 0. And lastly, we see a long spike again. Therefore, we end with an 1. And we get the binary number 101 for our y. This equals 5 in decimal, which is correct.

Let us do another one, now without knowing the answer beforehand. Take a look at Figure 2.

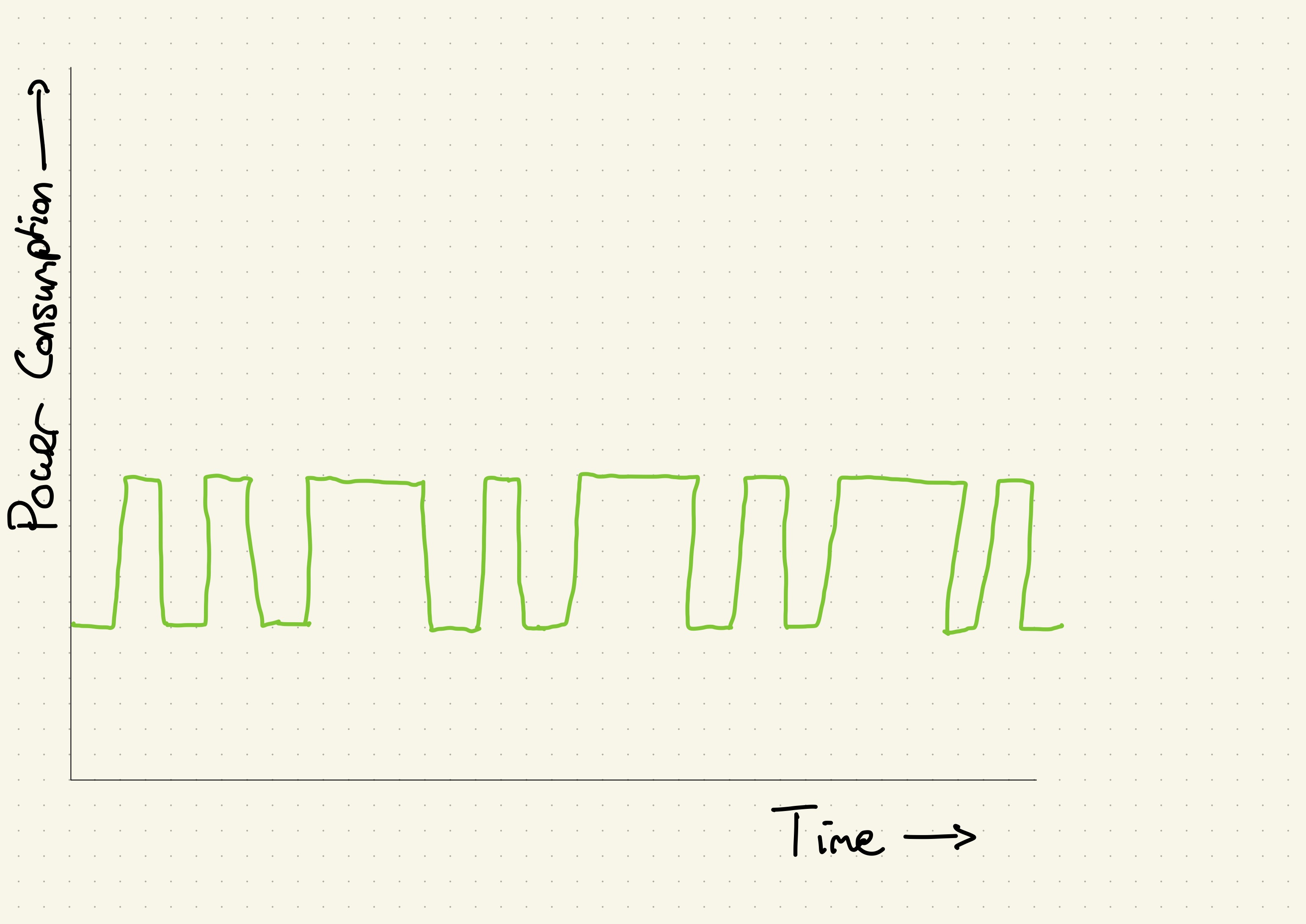
Figure 2: A projected power trace for the custom_pow_mod function.

We start with two short spikes, and thus we start with two zeros. Then we alternate a long spike with a short spike three times. This means we get 00101010. This is equal to decimal 42. And thus the y we started with is 42.

What does this tell us?

The previous code example may seem cherry-picked. In fact, it is not. This code snippet does, however, indicate the concept of Power analysis very nicely and is therefore a fantastic visual example of how to break an RSA implementation. Code following the same principle or even this exact algorithm is extremely common. This means that whilst this exact method may not be applicable everywhere, the underlying idea still is.

So whilst this method specifically is interesting, we are more interested in whether looking into an algorithm can tell us something about data used from the patterns in a power trace. In the next chapter, we are going through how this can be done with AES.